SDCTIE GRACELI EM FÍSICA ESTOCÁSTICA EM CADEIAS E PROGRESSIMAL TEMPORAL.

ONDE CADA UM FAZ A SUA PARTE [COMO AS CORES E OS JOGADORES CORRENDO], MAS UM INTERAGE E ALTERA O OUTRO. OU SEJA, EM CADEIAS E PROGRESSIMAL.

É COMO UMA AVALANCHE. OU EFEITO BORBOLETA USANDO DOMINÓS.

OU SEJA, E VARIAM CONFORME O SDCTIE GRACELI.

ONDE SE TEM COM ISTO UM CÁLCULO E UMA TOPOLOGIA GEOMÉTRICO E FÍSICA E UM SISTEMA DE CAMINHOS COM VARIAÇÕES EM CADEIAS E PROGRESSIMAL, DIFERENTE DA DE Feynman.

OU SEJA, SDCTIE GRACELI

X

A fórmula de Feynman–Kac, que recebe este nome em homenagem ao físico norte-americano Richard Feynman e ao matemático polonês Mark Kac, estabelece uma ligação entre equações diferenciais parciais (EDPs) parabólicas e processos estocásticos. A fórmula oferece um método para resolver algumas EDPs pela simulação de caminhos aleatórios de um processo estocástico. Reciprocamente, uma importante classe de valores esperados de processos aleatórios pode ser computada por métodos determinísticos.

Índice

• 1Fórmula
• 2Prova
• 3Considerações
• 4Ver também
• 5Referências

Fórmula

Considere a equação diferencial parcial^[1]

${\displaystyle {\frac {\partial u}{\partial t}}(x,t)+\mu (x,t){\frac {\partial u}{\partial x}}(x,t)+{\tfrac {1}{2}}\sigma ^{2}(x,t){\frac {\partial ^{2}u}{\partial x^{2}}}(x,t)-V(x,t)u(x,t)+f(x,t)=0,}$

definida para todo ${\displaystyle x}$ em R e todo ${\displaystyle t}$ em ${\displaystyle [0,T]}$, sujeita à condição terminal

${\displaystyle u(x,T)=\psi (x),}$

em que ${\displaystyle \mu }$, ${\displaystyle \sigma }$, ${\displaystyle \psi }$, ${\displaystyle V}$ e ${\displaystyle f}$ são funções conhecidas. ${\displaystyle T}$ é um parâmetro e ${\displaystyle u:\mathbb {R} \times [0,T]\to \mathbb {R} }$ é desconhecido. Então, a fórmula de Feynman–Kac nos diz que a solução pode ser escrita como um valor esperado condicional

${\displaystyle u(x,t)=E^{Q}\left[\int _{t}^{T}e^{-\int _{t}^{r}V(X_{\tau },\tau )\,d\tau }f(X_{r},r)dr+e^{-\int _{t}^{T}V(X_{\tau },\tau )\,d\tau }\psi (X_{T}){\Bigg |}X_{t}=x\right]}$

sob a medida de probabilidade ${\displaystyle Q}$, tal que ${\displaystyle X}$ é um processo de Itō dirigido pela equação

${\displaystyle dX=\mu (X,t)\,dt+\sigma (X,t)\,dW^{Q},}$

sendo ${\displaystyle W^{Q}(t)}$ um processo de Wiener (também chamado de movimento browniano) sob ${\displaystyle Q}$ e ${\displaystyle x}$ a condição inicial para ${\displaystyle X(t)}$.

Prova

Considere ${\displaystyle u(x,t)}$ a solução da EDP acima. Aplicando o lema de Itō ao processo^[2]

${\displaystyle Y(s)=e^{-\int _{t}^{s}V(X_{\tau },\tau )\,d\tau }u(X_{s},s)+\int _{t}^{s}e^{-\int _{t}^{r}V(X_{\tau },\tau )\,d\tau }f(X_{r},r)\,dr}$

obtém-se

${\displaystyle {\begin{aligned}dY={}&d\left(e^{-\int _{t}^{s}V(X_{\tau },\tau )\,d\tau }\right)u(X_{s},s)+e^{-\int _{t}^{s}V(X_{\tau },\tau )\,d\tau }\,du(X_{s},s)\\[6pt]&{}+d\left(e^{-\int _{t}^{s}V(X_{\tau },\tau )\,d\tau }\right)du(X_{s},s)+d\left(\int _{t}^{s}e^{-\int _{t}^{r}V(X_{\tau },\tau )\,d\tau }f(X_{r},r)\,dr\right)\end{aligned}}}$

Já que

${\displaystyle d\left(e^{-\int _{t}^{s}V(X_{\tau },\tau )\,d\tau }\right)=-V(X_{s},s)e^{-\int _{t}^{s}V(X_{\tau },\tau )\,d\tau }\,ds,}$

o terceiro termo é ${\displaystyle O(dt\,du)}$ e pode ser dispensado. Tem-se também que

${\displaystyle d\left(\int _{t}^{s}e^{-\int _{t}^{r}V(X_{\tau },\tau )\,d\tau }f(X_{r},r)dr\right)=e^{-\int _{t}^{s}V(X_{\tau },\tau )\,d\tau }f(X_{s},s)ds.}$

Aplicado o lema de Itō novamente a ${\displaystyle du(X_{s},s)}$, segue-se que

${\displaystyle {\begin{aligned}dY={}&e^{-\int _{t}^{s}V(X_{\tau },\tau )\,d\tau }\,\left(-V(X_{s},s)u(X_{s},s)+f(X_{s},s)+\mu (X_{s},s){\frac {\partial u}{\partial X}}+{\frac {\partial u}{\partial s}}+{\tfrac {1}{2}}\sigma ^{2}(X_{s},s){\frac {\partial ^{2}u}{\partial X^{2}}}\right)\,ds\\[6pt]&{}+e^{-\int _{t}^{s}V(X_{\tau },\tau )\,d\tau }\sigma (X,s){\frac {\partial u}{\partial X}}\,dW.\end{aligned}}}$

O primeiro termo contém, entre parênteses, a EDP acima, sendo portanto zero. O que sobra é

${\displaystyle dY=e^{-\int _{t}^{s}V(X_{\tau },\tau )\,d\tau }\sigma (X,s){\frac {\partial u}{\partial X}}\,dW.}$

Integrando esta equação de ${\displaystyle t}$ a ${\displaystyle T}$, conclui-se que

${\displaystyle Y(T)-Y(t)=\int _{t}^{T}e^{-\int _{t}^{s}V(X_{\tau },\tau )\,d\tau }\sigma (X,s){\frac {\partial u}{\partial X}}\,dW.}$

Ao tomar valores esperados, condicionados em ${\displaystyle X_{t}=x}$, observando que o lado direito é uma integral de Itō, que tem valor esperado zero, segue-se que

${\displaystyle E[Y(T)\mid X_{t}=x]=E[Y(t)\mid X_{t}=x]=u(x,t).}$

O resultado desejado é obtido observando que

${\displaystyle E[Y(T)\mid X_{t}=x]=E\left[e^{-\int _{t}^{T}V(X_{\tau },\tau )\,d\tau }u(X_{T},T)+\int _{t}^{T}e^{-\int _{t}^{r}V(X_{\tau },\tau )\,d\tau }f(X_{r},r)\,dr\,{\Bigg |}\,X_{t}=x\right]}$

e finalmente

${\displaystyle u(x,t)=E\left[e^{-\int _{t}^{T}V(X_{\tau },\tau )\,d\tau }\psi (X_{T})+\int _{t}^{T}e^{-\int _{t}^{s}V(X_{\tau },\tau )\,d\tau }f(X_{s},s)\,ds\,{\Bigg |}\,X_{t}=x\right]}$

Considerações

• A prova acima é essencialmente uma demonstração com modificações para computar ${\displaystyle f(x,t)}$.^[3]
• A fórmula de valor esperado acima também é válida para difusões de Itō de ${\displaystyle n}$ dimensões. A equação diferencial parcial correspondente para ${\displaystyle u:\mathbb {R} ^{N}\times [0,T]\to \mathbb {R} }$ se torna:^[4]

${\displaystyle {\frac {\partial u}{\partial t}}+\sum _{i=1}^{N}\mu _{i}(x,t){\frac {\partial u}{\partial x_{i}}}+{\frac {1}{2}}\sum _{i=1}^{N}\sum _{j=1}^{N}\gamma _{ij}(x,t){\frac {\partial ^{2}u}{\partial x_{i}x_{j}}}-r(x,t)u=f(x,t),}$

em que,

${\displaystyle \gamma _{ij}(x,t)=\sum _{k=1}^{N}\sigma _{ik}(x,t)\sigma _{jk}(x,t),}$

isto é, ${\displaystyle \gamma =\sigma \sigma '}$, em que ${\displaystyle \sigma '}$ denota a matriz transposta de ${\displaystyle \sigma )}$.

• O valor esperado pode ser então aproximado pelo método de Monte Carlo ou pelo método de quase-Monte Carlo.
• Quando foi publicado pela primeira vez por Kac em 1949, a fórmula de Feynman–Mac foi apresentada como uma fórmula para determinar a distribuição de certas funcionais de Wiener.^[5] Suponha que se deseja encontrar o valor esperado da função

${\displaystyle e^{-\int _{0}^{t}V(x(\tau ))\,d\tau }}$

no caso em que ${\displaystyle x(\tau )}$ é alguma ocorrência de um processo de difusão iniciado em ${\displaystyle x(0)=0}$. A fórmula de Feynman-Kac diz que o valor esperado é equivalente à integral de uma solução para uma equação de difusão. Especificamente, sob as condições de que${\displaystyle uV(x)\geq 0}$,

${\displaystyle E\left[e^{-u\int _{0}^{t}V(x(\tau ))\,d\tau }\right]=\int _{-\infty }^{\infty }w(x,t)\,dx}$

em que ${\displaystyle w(x,0)=\delta (x)}$ e

${\displaystyle {\frac {\partial w}{\partial t}}={\frac {1}{2}}{\frac {\partial ^{2}w}{\partial x^{2}}}-uV(x)w.}$

A fórmula de Feynman–Kac também pode ser interpretada como um método para avaliação de integrais funcionais de uma certa forma. Se

${\displaystyle I=\int f(x(0))e^{-u\int _{0}^{t}V(x(t))\,dt}g(x(t))\,Dx}$

em que a integral é tomada sobre todos os passeios aleatórios, então,

${\displaystyle I=\int w(x,t)g(x)\,dx}$

em que ${\displaystyle w(x,t)}$ é uma solução da equação diferencial parcial parabólica

${\displaystyle {\frac {\partial w}{\partial t}}={\frac {1}{2}}{\frac {\partial ^{2}w}{\partial x^{2}}}-uV(x)w}$

com a condição inicial ${\displaystyle w(x,0)=f(x)}$.

Em matemática, o lema de Itō é uma identidade usada em cálculo de Itō para encontrar a diferencial de uma função dependente do tempo de um processo estocástico. É o análogo em cálculo estocástico da regra da cadeia do cálculo comum. Pode ser heuristicamente derivado ao formar a expansão da série de Taylor de uma função, separando suas derivadas de segunda ordem e retendo termos até a primeira ordem no incremento do tempo e a segunda ordem no incremento de processo de Wiener. O lema é amplamente empregado em matemática financeira e sua aplicação mais conhecida é a derivação da equação de Black-Scholes para valores de opção.

O lema de Itō, que recebe este nome em homenagem a Kiyoshi Itō, é ocasionalmente referido como o teorema de Itō-Doeblin em reconhecimento ao trabalho postumamente descoberto de Wolfgang Döblin.^[1]

Enquanto o lema de Itō foi provado por Kiyoshi Itō, o teorema de Itō, um resultado em teoria dos grupos, recebe este nome devido a Noboru Itō.^[2]

Índice

• 1Derivação informal
• 2Formulação matemática do lema de Itō
  • 2.1Processos de tendência-difusão (drift-diffusion) de Itō
  • 2.2Processo de salto de Poisson
  • 2.3Semimartingales não contínuos
    • 2.3.1Processos de salto não contínuos múltiplos
• 3Exemplos
  • 3.1Movimento browniano geométrico
  • 3.2Exponencial de Doléans-Dade
  • 3.3Fórmula de Black-Scholes
• 4Ver também
• 5Referências

Derivação informal

Uma prova formal do lema se baseia em tomar o limite de uma sequência de variáveis aleatórias.^[3] Esta abordagem não é apresentada aqui, já que envolve uma série de detalhes técnicos. Em vez disto, segue abaixo um esboço de como se pode derivar o lema de Itō ao expandir uma série de Taylor e aplicar as regras do cálculo estocástico.

Considere X_t um processo de tendência-difusão de Itō que satisfaz à equação diferencial estocástica

${\displaystyle dX_{t}=\mu _{t}\,dt+\sigma _{t}\,dB_{t},}$

em que B_t é um processo de Wiener. Se f(t,x) for uma função escalar duplamente diferenciável, sua expansão em uma série de Taylor é

${\displaystyle df={\frac {\partial f}{\partial t}}\,dt+{\frac {\partial f}{\partial x}}\,dx+{\frac {1}{2}}{\frac {\partial ^{2}f}{\partial x^{2}}}\,dx^{2}+\cdots .}$

Substituindo X_t por x e μ_t dt + σ_t dB_t por dx temos

${\displaystyle df={\frac {\partial f}{\partial t}}\,dt+{\frac {\partial f}{\partial x}}(\mu _{t}\,dt+\sigma _{t}\,dB_{t})+{\frac {1}{2}}{\frac {\partial ^{2}f}{\partial x^{2}}}\left(\mu _{t}^{2}\,dt^{2}+2\mu _{t}\sigma _{t}\,dt\,dB_{t}+\sigma _{t}^{2}\,dB_{t}^{2}\right)+\cdots .}$

No limite dt → 0, os termos dt² e dt dB_t tendem a zero mais rapidamente que dB², que é O(dt). Configurando os termos dt² e dt dB_t a zero, substituindo dt por dB² e coletando os termos dt e dB, obtemos

${\displaystyle df=\left({\frac {\partial f}{\partial t}}+\mu _{t}{\frac {\partial f}{\partial x}}+{\frac {\sigma _{t}^{2}}{2}}{\frac {\partial ^{2}f}{\partial x^{2}}}\right)dt+\sigma _{t}{\frac {\partial f}{\partial x}}\,dB_{t}}$

como exigido.

Formulação matemática do lema de Itō

Nas subseções seguintes, são discutidas versões de lema de Itō para diferentes tipos de processos estocásticos.^[4]

Processos de tendência-difusão (drift-diffusion) de Itō

Em sua forma mais simples, o lema de Itō afirma que, para um processo de tendência-difusão de Itō^[5]

${\displaystyle dX_{t}=\mu _{t}\,dt+\sigma _{t}\,dB_{t}}$

em que ${\displaystyle dB_{t}}$ é a diferencial do movimento Browniano. Para qualquer função escalar duplamente diferenciável f(t,x) de duas variáveis reais t e x, tem-se

${\displaystyle df(t,X_{t})=\left({\frac {\partial f}{\partial t}}+\mu _{t}{\frac {\partial f}{\partial x}}+{\frac {\sigma _{t}^{2}}{2}}{\frac {\partial ^{2}f}{\partial x^{2}}}\right)dt+\sigma _{t}{\frac {\partial f}{\partial x}}\,dB_{t}.}$

Isto imediatamente implica que f(t,X_t) é um processo de tendência-difusão de Itō.

Em dimensões mais elevadas, se ${\displaystyle \mathbf {X} _{t}=(X_{t}^{1},X_{t}^{2},\ldots ,X_{t}^{n})^{T}}$ é um vetor de processo de Itō,^[6] tal que

${\displaystyle d\mathbf {X} _{t}={\boldsymbol {\mu }}_{t}\,dt+\mathbf {G} _{t}\,d\mathbf {B} _{t}}$

para um vetor ${\displaystyle {\boldsymbol {\mu }}_{t}}$ e uma matriz ${\displaystyle \mathbf {G} _{t}}$, o lema de Itō afirma então que

${\displaystyle {\begin{aligned}df(t,\mathbf {X} _{t})&={\frac {\partial f}{\partial t}}\,dt+\left(\nabla _{\mathbf {X} }f\right)^{T}\,d\mathbf {X} _{t}+{\frac {1}{2}}\left(d\mathbf {X} _{t}\right)^{T}\left(H_{\mathbf {X} }f\right)\,d\mathbf {X} _{t},\\&=\left\{{\frac {\partial f}{\partial t}}+\left(\nabla _{\mathbf {X} }f\right)^{T}{\boldsymbol {\mu }}_{t}+{\frac {1}{2}}{\text{Tr}}\left[\mathbf {G} _{t}^{T}\left(H_{\mathbf {X} }f\right)\mathbf {G} _{t}\right]\right\}dt+\left(\nabla _{\mathbf {X} }f\right)^{T}\mathbf {G} _{t}\,d\mathbf {B} _{t}\end{aligned}}}$

em que ∇_X f é o gradiente de f em relação a X, H_X f é a matriz hessiana de f em relação a X, e Tr é o operador traço.

Processo de salto de Poisson

Também é possível definir funções relativas a processos estocásticos descontínuos.^[7]

Considere h a densidade do salto. O modelo de processo de Poisson para saltos diz que a probabilidade de um salto no intervalo [t, t + Δt] é hΔt mais termos de ordem mais elevada. h pode ser uma constante, uma função determinística do tempo ou um processo estocástico. A probabilidade de sobrevivência p_s(t) é a probabilidade de que nenhum salto ocorra no intervalo [0, t]. A mudança na probabilidade de sobrevivência é

${\displaystyle dp_{s}(t)=-p_{s}(t)h(t)\,dt.}$

Então

${\displaystyle p_{s}(t)=\exp \left(-\int _{0}^{t}h(u)\,du\right).}$

Considere S(t) um processo estocástico descontínuo. ${\displaystyle S(t^{-})}$ é o valor de ${\displaystyle S}$ conforme se aproxima ${\displaystyle t}$ a partir da esquerda. ${\displaystyle d_{j}S(t)}$ é a mudança não infinitesimal em S(t) como um resultado de um salto. Então

${\displaystyle d_{j}S(t)=\lim _{\Delta t\to 0}(S(t+\Delta t)-S(t^{-}))}$

Considere ${\displaystyle z}$ a magnitude do salto e ${\displaystyle \eta (S(t^{-}),z)}$ a distribuição de probabilidade de ${\displaystyle z}$. A magnitude esperada do salto é

${\displaystyle E[d_{j}S(t)]=h(S(t^{-}))\,dt\int _{z}z\eta (S(t^{-}),z)\,dz.}$

Defina ${\displaystyle dJ_{S}(t)}$, um processo compensado e martingale, como

${\displaystyle dJ_{S}(t)=d_{j}S(t)-E[d_{j}S(t)]=S(t)-S(t^{-})-\left(h(S(t^{-}))\int _{z}z\eta \left(S(t^{-}),z\right)\,dz\right)\,dt.}$

Então

${\displaystyle d_{j}S(t)=E[d_{j}S(t)]+dJ_{S}(t)=h(S(t^{-}))\left(\int _{z}z\eta (S(t^{-}),z)\,dz\right)dt+dJ_{S}(t).}$

Considere uma função ${\displaystyle g(S(t),t)}$ do processo de salto dS(t). Se S(t) salta Δs, então g(t) salta Δg. Δg é tirado da distribuição ${\displaystyle \eta _{g}()}$ que pode depender de ${\displaystyle g(t^{-})}$, dg e ${\displaystyle S(t^{-})}$. A parte de salto de ${\displaystyle g}$ é

${\displaystyle g(t)-g(t^{-})=h(t)\,dt\int _{\Delta g}\,\Delta g\eta _{g}(\cdot )\,d\Delta g+dJ_{g}(t).}$

Se ${\displaystyle S}$ contém tendência, difusão e salto, então o lema de Itō para ${\displaystyle g(S(t),t)}$ é

${\displaystyle dg(t)=\left({\frac {\partial g}{\partial t}}+\mu {\frac {\partial g}{\partial S}}+{\frac {\sigma ^{2}}{2}}{\frac {\partial ^{2}g}{\partial S^{2}}}+h(t)\int _{\Delta g}\left(\Delta g\eta _{g}(\cdot )\,d{\Delta }g\right)\,\right)dt+{\frac {\partial g}{\partial S}}\sigma \,dW(t)+dJ_{g}(t).}$

O lema de Itō para um processo que é a soma de processo de tendência-difusão e um processo de salto é simplesmente a soma do lema de Itō para as partes individuais.

Semimartingales não contínuos

O lema de Itō também pode ser aplicado a semimartingales gerais de ${\displaystyle d}$ dimensões, que não precisam ser contínuos.^[8] Em geral, um semimartingale é um processo càdlàg e um termo adicional precisa ser adicionado à fórmula para garantir que os saltos do processo estejam corretamente dados pelo lema de Itō. Para qualquer processo càdlàg Y_t, o limite à esquerda em ${\displaystyle t}$ é denotado por Y_t−, que é um processo contínuo à esquerda. Os saltos são escritos como ΔY_t = Y_t − Y_t−. Então, o lema de Itō afirma que, se X = (X¹, X², ..., X^d) for um semimartingale de ${\displaystyle d}$ dimensões e ${\displaystyle f}$ for uma função de valores reais duplamente e continuamente diferenciável em R^d, então, ${\displaystyle f(X)}$ é um semimartingale e

${\displaystyle {\begin{aligned}f(X_{t})&=f(X_{0})+\sum _{i=1}^{d}\int _{0}^{t}f_{i}(X_{s-})\,dX_{s}^{i}+{\frac {1}{2}}\sum _{i,j=1}^{d}\int _{0}^{t}f_{i,j}(X_{s-})\,d[X^{i},X^{j}]_{s}\\&\qquad +\sum _{s\leq t}\left(\Delta f(X_{s})-\sum _{i=1}^{d}f_{i}(X_{s-})\,\Delta X_{s}^{i}-{\frac {1}{2}}\sum _{i,j=1}^{d}f_{i,j}(X_{s-})\,\Delta X_{s}^{i}\,\Delta X_{s}^{j}\right).\end{aligned}}}$

Isto difere da fórmula para semimartingales contínuos pelo termo adicional somando ao longo dos saltos de ${\displaystyle X}$, garantindo que o salto do lado direito no tempo ${\displaystyle t}$ seja ${\displaystyle \Delta f(X_{t})}$.

Processos de salto não contínuos múltiplos

Também há uma versão disto para um função ${\displaystyle f}$ duplamente e continuamente diferenciável no espaço e unicamente diferenciável no tempo avaliado em semimartingales (potencialmente diferentes) não contínuos que pode ser escrita da seguinte forma:

${\displaystyle {\begin{aligned}f(t,X_{t}^{1},...,X_{t}^{d})&=f(0,X_{0}^{1},...,X_{0}^{d})+\int _{0}^{t}{\dot {f}}({s_{-}},X_{s_{-}}^{1},...,X_{s_{-}}^{d})d{s}\\&+\sum _{i=1}^{n}\int _{0}^{t}f_{i}({s_{-}},X_{s_{-}}^{1},...,X_{s_{-}}^{d})\,dX_{s}^{(c,i)}\\&+{\frac {1}{2}}\sum _{i_{1},..,i_{d}=1}^{d}\int _{0}^{t}f_{i_{1},..,i_{d}}({s_{-}},X_{s_{-}}^{1},...,X_{s_{-}}^{d})\,dX_{s}^{(c,i_{1})}...X_{s}^{(c,i_{d})}\\&+\sum _{0<s\leq t}\left[f(s,X_{s}^{1},...,X_{s}^{d})-f({s_{-}},X_{s_{-}}^{1},...,X_{s_{-}}^{d})\right]\end{aligned}}}$

Em que ${\displaystyle X^{c,i}}$ denota a parte contínua do ${\displaystyle i}$-ésimo semimartingale.

Exemplos

Movimento browniano geométrico

Um processo ${\displaystyle S}$ segue um movimento browniano geométrico com volatilidade constante ${\displaystyle \sigma }$ e deriva constante ${\displaystyle \mu }$ se satisfizer à equação diferencial estocástica dS = S(σdB + μdt) para um movimento browniano ${\displaystyle B}$. Aplicando-se o lema de Itō com ${\displaystyle f(S)=log(S)}$, temos

${\displaystyle {\begin{aligned}d\log(S)&=f^{\prime }(S)\,dS+{\frac {1}{2}}f^{\prime \prime }(S)S^{2}\sigma ^{2}\,dt\\&={\frac {1}{S}}\left(\sigma S\,dB+\mu S\,dt\right)-{\frac {1}{2}}\sigma ^{2}\,dt\\&=\sigma \,dB+\left(\mu -{\tfrac {\sigma ^{2}}{2}}\right)\,dt.\end{aligned}}}$

Segue-se disto

${\displaystyle \log(S_{t})=\log(S_{0})+\sigma B_{t}+\left(\mu -{\tfrac {\sigma ^{2}}{2}}\right)t,}$

e a exponenciação dá para ${\displaystyle S}$ a expressão

${\displaystyle S_{t}=S_{0}\exp \left(\sigma B_{t}+\left(\mu -{\tfrac {\sigma ^{2}}{2}}\right)t\right).}$

O tempo de correção de − σ²2 corresponde à diferença entre a mediana e a média da distribuição log-normal ou, equivalentemente a esta distribuição, a média geométrica e a média aritmética, sendo a mediana (média geométrica) mais baixa. Isto se deve à desigualdade das médias e corresponde ao logaritmo sendo convexo para baixo, então o termo de correção pode, portanto, ser interpretado como uma correção de convexidade. Isto é uma versão infinitesimal do fato de que o retorno anualizado é menor que o retorno médio, sendo diferença proporcional à variância.

O mesmo fator de σ²2 aparece nas variáveis auxiliares ${\displaystyle d_{1}}$ e ${\displaystyle d_{2}}$ da fórmula de Black-Scholes e pode ser interpretado como uma consequência do lema de Itō.

Exponencial de Doléans-Dade

O exponencial de Doléans-Dade (ou exponencial estocástico) de um semimartingale contínuo ${\displaystyle X}$ pode ser definido como a solução da equação diferencial estocástica dY = Y dX com condição inicial Y₀ = 1. É às vezes denotado como Ɛ(X). Aplicando-se o lema de Itō com ${\displaystyle f(Y)=log(Y)}$, temos

${\displaystyle {\begin{aligned}d\log(Y)&={\frac {1}{Y}}\,dY-{\frac {1}{2Y^{2}}}\,d[Y]\\&=dX-{\tfrac {1}{2}}\,d[X].\end{aligned}}}$

A exponenciação dá a solução

${\displaystyle Y_{t}=\exp \left(X_{t}-X_{0}-{\tfrac {1}{2}}[X]_{t}\right).}$

Fórmula de Black-Scholes

O lema de Itō pode ser usado para derivar a fórmula de Black-Scholes para uma opção.^[9] Suponha que o preço de uma ação segue um movimento browniano geométrico dado pela equação diferencial estocástica dS = S(σdB + μ dt). Então, se o valor de uma opção no tempo ${\displaystyle t}$ for ${\displaystyle f(t,S_{t})}$, o lema de Itō dá

${\displaystyle df(t,S_{t})=\left({\frac {\partial f}{\partial t}}+{\frac {1}{2}}\left(S_{t}\sigma \right)^{2}{\frac {\partial ^{2}f}{\partial S^{2}}}\right)\,dt+{\frac {\partial f}{\partial S}}\,dS_{t}.}$

O termo ${\displaystyle {\frac {\partial f}{\partial S}}\,dS_{t}}$ representa a variação no valor no tempo ${\displaystyle dt}$ da estratégia de negociação que consiste em manter em carteira uma quantidade ${\displaystyle {\frac {\partial f}{\partial S}}}$ da ação. Seguindo essa estratégia e considerando que qualquer quantidade de dinheiro mantida é remunerada à taxa livre de risco ${\displaystyle r}$, então o valor total ${\displaystyle V}$ deste portfólio satisfaz à equação diferencial estocástica

${\displaystyle dV_{t}=r\left(V_{t}-{\frac {\partial f}{\partial S}}S_{t}\right)\,dt+{\frac {\partial f}{\partial S}}\,dS_{t}.}$

Esta estratégia replica a opção se ${\displaystyle V=f(t,S)}$. A combinação destas equações resulta na famosa equação de Black-Scholes

${\displaystyle {\frac {\partial f}{\partial t}}+{\frac {\sigma ^{2}S^{2}}{2}}{\frac {\partial ^{2}f}{\partial S^{2}}}+rS{\frac {\partial f}{\partial S}}-rf=0.}$

Teorema de Girsanov

Origem: Wikipédia, a enciclopédia livre.

Saltar para a navegaçãoSaltar para a pesquisa

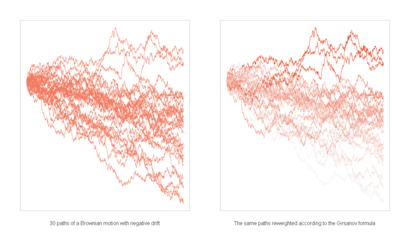
Visualização do teorema de Girsanov. O lado esquerdo mostra um processo de Wiener negativo; do lado direito, cada etapa do processo está colorido de acordo com a probabilidade na medida Q. A densidade de transformação de P a Q é dada pelo teorema de Girsanov.

Na teoria da probabilidade, o teorema de Girsanov (em nome de Igor Vladimirovich Girsanov) descreve como a dinâmica de processos estocásticos muda quando o a medida original é alterada para uma medida da probabilidade equivalente.^[1]:607 O teorema é especialmente importante na teoria da matemática financeira, na medida em que converte a probabilidade de uma medida física que descreve a probabilidade de que um ativo subjacente (como um preço ou uma taxa de juros) ter um determinado valor ou valores em uma medida de risco-neutro, uma uma ferramenta muito útil para o cálculo de preços derivados do subjacente.

Índice

• 1História
• 2Significado
• 3Demonstração do teorema
• 4Veja também
• 5Referências
• 6Ligações externas

História

Resultados deste tipo foram pela primeira vez demonstrados por Cameron–Martin na década de 1940 e por Girsanov, em 1960.^[2] Eles foram, posteriormente, estendido para classes mais gerais de processo que culminaram na forma geral de Lenglart (1977).

Significado

O teorema de Girsanov é importante na teoria geral de processos estocásticos, pois permite que o resultado-chave de que se Q é uma medida absolutamente contínua com respeito a P , então, todo P-semimartingale é um Q-semimartingale.^[3]

Demonstração do teorema

Apresentamos o teorema primeiro para o caso especial quando o processo estocástico subjacente é um processo de Wiener. Este caso especial é suficiente para preços de risco-neutro no modelo de Black-Scholes e em muitos outros modelos (por exemplo, modelos contínuos).

Deixe ${\displaystyle \{W_{t}\}}$ ser um processo de Wiener espaço de probabilidade Wiener ${\displaystyle \{\Omega ,{\mathcal {F}},P\}}$. Deixe ${\displaystyle X_{t}}$ ser um processo adaptado mensurável para a filtragem natural do processo de Wiener${\displaystyle \{{\mathcal {F}}_{t}^{W}\}}$ com ${\displaystyle X_{0}=0}$.

Defina o exponencial Doléans ${\displaystyle {\mathcal {E}}(X)_{t}}$ de X com respeito a W

${\displaystyle {\mathcal {E}}(X)_{t}=\exp \left(X_{t}-{\frac {1}{2}}[X]_{t}\right),}$

Se ${\displaystyle {\mathcal {E}}(X)_{t}}$ é um martingale estritamente positivo, uma medida de probabilidade Q pode ser definida em ${\displaystyle \{\Omega ,{\mathcal {F}}\}}$ de tal forma a termos um derivativo de de Radon–Nikodym

${\displaystyle {\frac {dQ}{dP}}|_{{\mathcal {F}}_{t}}={\mathcal {E}}(X)_{t}}$

Em seguida, para cada t a medida Q restrita para os campos sigma não aumentados ${\displaystyle {\mathcal {F}}_{t}^{W}}$ é equivalente a P restrito a ${\displaystyle {\mathcal {F}}_{t}^{W}}$. Além disso, se Y é um local de martingale em P, então o processo

${\displaystyle {\tilde {Y}}_{t}=Y_{t}-\left[Y,X\right]_{t}}$

é um Q local de martingale no espaço de probabilidade filtrado ${\displaystyle \{\Omega ,F,Q,\{F_{t}^{W}\}\}}$.

Movimento browniano fracionário

Origem: Wikipédia, a enciclopédia livre.

Saltar para a navegaçãoSaltar para a pesquisa

Em teoria das probabilidades, o movimento browniano fracionário (MBF), também chamado de movimento browniano fractal, é uma generalização do movimento browniano. Diferentemente do movimento browniano clássico, os incrementos do MBF não precisam ser independentes.^[1] O MBF é um processo gaussiano de tempo contínuo ${\displaystyle B_{H}(t)}$ em ${\displaystyle [0,T]}$, que começa em zero, tem valor esperado zero para todo ${\displaystyle t}$ em ${\displaystyle [0,T]}$ e possui a seguinte função de covariância:

${\displaystyle E[B_{H}(t)B_{H}(s)]={\tfrac {1}{2}}(|t|^{2H}+|s|^{2H}-|t-s|^{2H}),}$

em que ${\displaystyle H}$ é um número real em ${\displaystyle (0,1)}$, chamado de índice de Hurst ou parâmetro de Hurst, associado com o movimento browniano fracionário. O expoente de Hurst descreve a irregularidade do movimento resultante, sendo que um valor maior leva a um movimento mais suave. Foi introduzido por Benoit Mandelbrot and John W. Van Ness em 1968.^[2]

O valor de ${\displaystyle H}$ determina o tipo de processo do MBF:

• Se ${\displaystyle H=1/2}$, então, o processo é de fato um movimento browniano ou um processo de Wiener;
• Se ${\displaystyle H>1/2}$, então, os incrementos do processo estão positivamente correlacionados;
• Se ${\displaystyle H<1/2}$, então, os incrementos do processo são negativamente correlacionados.

O processo do incremento, ${\displaystyle X(t)=B_{H}(t+1)-B_{H}(t)}$, é conhecido como ruído gaussiano fracionário.

Há também uma generalização do movimento browniano fracionário, o movimento browniano fracionário de n-ésima ordem (MBF-n).^[3] O MBF-n é um processo gaussiano, autossimilar, não estacionário cujos incrementos de ordem ${\displaystyle n}$ são estacionários. Para ${\displaystyle n=1}$, o MBF-n é um MBF clássico.

Assim como o movimento browniano que generaliza, o movimento browniano fracionário recebe este nome em homenagem ao botânico escocês Robert Brown. O ruído gaussiano fracionário recebe este nome em homenagem ao matemático alemão Carl Friedrich Gauss.

Índice

• 1Plano de fundo e definição
• 2Propriedades
  • 2.1Autossimilaridade
  • 2.2Incrementos estacionários
  • 2.3Dependência de longo intervalo
  • 2.4Regularidade
  • 2.5Dimensão
  • 2.6Integração
  • 2.7Interpretação do domínio de frequência
• 3Caminhos amostrais
  • 3.1Método 1 de simulação
  • 3.2Método 2 de simulação
• 4Ver também
• 5Referências

Plano de fundo e definição

Antes da introdução do movimento browniano fracionário, Paul Lévy usou em 1953 a integral fracionária de Riemann–Liouville para definir o processo:^[4]

${\displaystyle B_{H}(t)={\frac {1}{\Gamma (H+1/2)}}\int _{0}^{t}(t-s)^{H-1/2}\,dB(s),}$

em que a integração é em relação à medida de ruído branco ${\displaystyle dB(s)}$. Esta integral se revelou inadequada para aplicações do movimento browniano fracionário devido a sua ênfase excessiva na origem.^[2]

Em vez disso, a ideia é usar uma integral fracionária de ruído branco diferente para definir o processo, a integral de Weyl:

${\displaystyle B_{H}(t)=B_{H}(0)+{\frac {1}{\Gamma (H+1/2)}}\left\{\int _{-\infty }^{0}\left[(t-s)^{H-1/2}-(-s)^{H-1/2}\right]\,dB(s)+\int _{0}^{t}(t-s)^{H-1/2}\,dB(s)\right\},}$

para ${\displaystyle t>0}$ (e, da mesma forma, para ${\displaystyle t<0}$).

A principal diferença entre o movimento browniano fracionário e o movimento browniano regular é que, enquanto os incrementos no movimento browniano são independentes, o oposto se aplica ao movimento browniano fracionário. Esta dependência significa que, se houver um padrão crescente nos passos anteriores, então, é provável que o passo seguinte também seja crescente (se ${\displaystyle H>1/2}$).

Propriedades

Autossimilaridade

O processo é autossimilar, já que em termos de distribuições de probabilidade:^[5]

${\displaystyle B_{H}(at)\sim |a|^{H}B_{H}(t).}$

Esta propriedade se deve ao fato de que a função de covariância é homogênea de ordem ${\displaystyle 2H}$ e pode ser considerada uma propriedade fractal. O movimento browniano fracionário é o único processo gaussiano autossimilar.

Incrementos estacionários

O movimento browniano fracionário tem incrementos estacionários:

${\displaystyle B_{H}(t)-B_{H}(s)\sim B_{H}(t-s).}$

Dependência de longo intervalo

Para ${\displaystyle H>1/2}$, o processo exibe dependência de longo intervalo:^[6]

${\displaystyle \sum _{n=1}^{\infty }E[B_{H}(1)(B_{H}(n+1)-B_{H}(n))]=\infty .}$

Regularidade

Caminhos amostrais são diferenciáveis em quase lugar nenhum. Entretanto, quase todas as trajetórias são contínuas de Hölder de qualquer ordem estritamente menor que ${\displaystyle H}$. Para cada trajetória deste tipo, para todo ${\displaystyle T>0}$ e para todo ${\displaystyle \varepsilon >0}$, existe uma constante ${\displaystyle c}$, tal que:

${\displaystyle |B_{H}(t)-B_{H}(s)|\leq c|t-s|^{H-\varepsilon },}$

para ${\displaystyle 0<s,t<T}$.

Dimensão

Com probabilidade 1, o gráfico de ${\displaystyle B_{H}(t)}$ tem tanto dimensão de Hausdorff, como dimensão de caixa igual a ${\displaystyle 2-H}$.

Integração

Assim como para o movimento browniano regular, é possível definir integrais estocásticas em relação ao movimento browniano fracionário, comumente chamadas de "integrais estocásticas fracionárias". Em geral, no entanto, diferentemente de integrais em relação ao movimento browniano regular, integrais estocásticas fracionárias não são semimartingales.

Interpretação do domínio de frequência

Assim como o movimento browniano tem ruído branco filtrado por ${\displaystyle s^{-1}}$ (isto é, integrado), o movimento browniano fracionário tem ruído branco filtrado por ${\displaystyle s^{-H-1/2}}$ (correspondente à integração fracionária).

Caminhos amostrais

Ocorrências práticas em computador de um MBF podem ser geradas, ainda que sejam apenas uma aproximação finita.^[7] Pode-se pensar que os caminhos amostrais mostram pontos amostrais discretos em um processo de MBF. Estas ocorrências são mostradas abaixo, cada uma com 1.000 pontos de um MBF com parâmetro de Hurst 0,75.

${\displaystyle H=0,75}$, ocorrência 1

${\displaystyle H=0,75}$, ocorrência 2

${\displaystyle H=0,75}$, ocorrência 3

Ocorrência de três tipos diferentes de MBF são mostradas abaixo, cada uma mostrando 1.000 pontos. A primeira tem parâmetro de Hurst igual a 0,15. A segunda tem parâmetro de Hurst igual a 0,55. A terceira tem parâmetro de Hurst igual a 0,95. Quanto mais alto o parâmetro de Hurst, mais suave será a curva.

${\displaystyle H=0,15}$

${\displaystyle H=0,55}$

${\displaystyle H=0,95}$

Método 1 de simulação

É possível simular caminhos amostrais de um MBF pelo uso de métodos que geram processos gaussianos estacionários com função de covariância conhecida.^[8] O método mais simples tem como base o método de decomposição de Cholesky da matriz de covariância, que, em uma grade de tamanho ${\displaystyle n}$, tem complexidade de ordem ${\displaystyle O(n^{3})}$.^[9] Um método mais complexo, mas computacionalmente mais rápido é o método do encaixe circulante proposto por C. R. Dietrich e G. N. Newsam em 1997.^[10]

Suponha que queremos simular os valores do MBF nos tempos ${\displaystyle t_{1},...,t_{n}}$, usando o método da decomposição de Cholesky.

• Forme a matriz ${\displaystyle \Gamma ={\bigl (}R(t_{i},t_{j}),i,j=1,...,n{\bigr )}}$ em que ${\displaystyle R(t,s)=(s^{2H}+t^{2H}-|t-s|^{2H})/2}$;
• Compute ${\displaystyle \Sigma }$ a matriz da raiz quadrada de ${\displaystyle \Gamma }$, isto é, ${\displaystyle \Sigma ^{2}=\Gamma }$. Falando livremente, ${\displaystyle \Sigma }$ é a matriz de "desvio padrão" associada à matriz de variância-covariância ${\displaystyle \Gamma }$;
• Construa um vetor ${\displaystyle v}$ de ${\displaystyle n}$ números obtidos independentemente de acordo com uma distribuição gaussiana padrão;
• Se definirmos ${\displaystyle u=\Sigma v}$, então, ${\displaystyle u}$ produz um caminho amostral de um MBF.

Para computar ${\displaystyle \Sigma }$, pode-se usar por exemplo o método de decomposição de Cholesky. Um método alternativo usa os autovalores de ${\displaystyle \Gamma }$:

• Já que ${\displaystyle \Gamma }$ é uma matriz simétrica e positiva definida, segue-se que todos os autovalores ${\displaystyle \lambda _{i}}$ de ${\displaystyle \Gamma }$ satisfazem ${\displaystyle \lambda _{i}\geq 0}$, ${\displaystyle (i=1,...,n)}$.
• Considere ${\displaystyle \Lambda }$ a matriz diagonal dos autovalores, isto é, ${\displaystyle \Lambda _{ij}=\lambda _{i}\delta _{ij}}$, em que ${\displaystyle \delta _{ij}}$ é o delta de Kronecker. Definimos ${\displaystyle \Lambda ^{1/2}}$ como a matriz diagonal com entradas ${\displaystyle \lambda _{i}^{1/2}}$, isto é, ${\displaystyle \Lambda _{ij}^{1/2}=\lambda _{i}^{1/2}\delta _{ij}}$.

Note que o resultado tem valores reais porque ${\displaystyle \lambda _{i}\geq 0}$

• Considere ${\displaystyle v_{i}}$ um autovalor associado com o autovalor ${\displaystyle \lambda _{i}}$. Defina ${\displaystyle P}$ como a matriz cuja ${\displaystyle i}$-ésima coluna é o autovalor ${\displaystyle v_{i}}$.

Note que, já que os autovalores são linearmente independentes, a matriz${\displaystyle \,P}$ é inversível.

• Segue-se então que ${\displaystyle \Sigma =P\Lambda ^{1/2}P^{-1}}$, porque ${\displaystyle \Gamma =P\Lambda P^{-1}}$.

Método 2 de simulação

Também se sabe que^[7]

${\displaystyle B_{H}(t)=\int _{0}^{t}K_{H}(t,s)dB(s),}$

em que ${\displaystyle B}$ é um movimento browniano padrão e

${\displaystyle K_{H}(t,s)={\frac {(t-s)^{H-{\frac {1}{2}}}}{\Gamma (H+{\frac {1}{2}})}}\;_{2}F_{1}\left(H-{\frac {1}{2}};{\frac {1}{2}}-H;H+{\frac {1}{2}};1-{\frac {t}{s}}\right),}$

em que ${\displaystyle _{2}F_{1}}$ é a integral hipergeométrica de Euler.

Se quisermos simular um MBF em pontos ${\displaystyle 0=t_{0}<t_{1}<...<t_{n}=T}$:

• Construa um vetor de ${\displaystyle n}$ números obtidos de acordo com uma distribuição gaussiana padrão;
• Multiplique-o por componentes por ${\displaystyle {\sqrt {(T/n)}}}$ para obter os incrementos de um movimento browniano em ${\displaystyle [0,T]}$. Denote este vetor por ${\displaystyle (\delta B_{1},...,\delta B_{n})}$;
• Para cada ${\displaystyle t_{j}}$, compute:

${\displaystyle B_{H}(t_{j})={\frac {n}{T}}\sum _{i=0}^{j-1}\int _{t_{i}}^{t_{i+1}}K_{H}(t_{j},s)ds\delta B_{i}.}$

A integral pode ser eficientemente computada pela quadratura gaussiana.

Movimento browniano geométrico

Origem: Wikipédia, a enciclopédia livre.

Saltar para a navegaçãoSaltar para a pesquisa

Dois caminhos de exemplo do movimento Browniano geométrico, com parâmetros diferentes. A linha azul tem maior deriva, a linha verde tem maior variância.

Um movimento browniano geométrico (MBG) (também conhecido como movimento geométrico browniano e movimento browniano exponencial) é um processo estocástico de tempo contínuo no qual o logaritmo da quantidade aleatoriamente variável segue um movimento browniano (também chamado de processo de Wiener), com deriva estocástica.^[1] É um exemplo importante de processos estocásticos que satisfazem uma equação diferencial estocástica (EDE); em particular, é usado em matemática financeira para o modelar os preços das ações no modelo Black–Scholes.

Índice

• 1Definição formal
• 2Solução da EDE
• 3Propriedades
• 4Versão multivariada 
• 5Uso em finanças
• 6Extensões
• 7Veja também
• 8Referências
• 9Ligações externas

Definição formal

Um processo estocástico S_t é dito seguir um MBG se ele satisfaz a seguinte equação diferencial estocástica (EDE):

${\displaystyle dS_{t}=\mu S_{t}\,dt+\sigma S_{t}\,dW_{t}}$

onde ${\displaystyle W_{t}}$ é um processo de Wiener ou movimento Browniano, e ${\displaystyle \mu }$ ("percentage drift" ou "percentagem de deriva") e ${\displaystyle \sigma }$ ("percentage volatility" ou "percentagem de volatilidade") são constantes.

O primeiro é utilizado para modelar tendências determinísticas, enquanto o último termo é muitas vezes usado para modelar um conjunto de eventos imprevisíveis que ocorrem durante este movimento.

Solução da EDE

Para um valor arbitrário inicial S₀ a EDE possui uma solução analítica (sob o cálculo de Itō):

${\displaystyle S_{t}=S_{0}\exp \left(\left(\mu -{\frac {\sigma ^{2}}{2}}\right)t+\sigma W_{t}\right)}$.

Para chegar a essa fórmula, dividiremos a EDE, por ${\displaystyle S_{t}}$ a fim de que nossa variável aleatória escolhida tenha apenas um lado. A partir daí podemos escrever a equação anterior na forma da integral de Itō:

${\displaystyle \int _{0}^{t}{\frac {dS_{t}}{S_{t}}}=\mu \,t+\sigma \,W_{t}\,,\qquad {\text{assumindo que }}W_{0}=0\,}$.

Claro, ${\displaystyle {\frac {dS_{t}}{S_{t}}}}$ aparenta ser relacionado à derivada de ${\displaystyle \ln S_{t}}$. No entanto, ${\displaystyle S_{t}}$ é um processo de Itō que requer o uso do cálculo de Itō. A aplicação da fórmula de Itō leva a:

${\displaystyle d(\ln S_{t})={\frac {dS_{t}}{S_{t}}}-{\frac {1}{2}}\,{\frac {1}{S_{t}^{2}}}\,dS_{t}dS_{t}}$

onde ${\displaystyle dS_{t}dS_{t}}$ é a variação quadrática da EDE. Isso também pode ser escrito como ${\displaystyle d[S]_{t}}$ ou ${\displaystyle \left\langle S_{.}\right\rangle _{t}\,}$. Neste caso, temos:

${\displaystyle dS_{t}dS_{t}\,=\,\sigma ^{2}\,S_{t}^{2}\,dt}$.

Substituindo o valor de ${\displaystyle dS_{t}}$ na equação acima e simplificando obtemosː

${\displaystyle \ln {\frac {S_{t}}{S_{0}}}=\left(\mu -{\frac {\sigma ^{2}}{2}}\,\right)t+\sigma W_{t}\,}$.

Tomando a exponencial e multiplicando ambos os lados por ${\displaystyle S_{0}}$ dá a solução reivindicada acima.

Propriedades

A solução acima ${\displaystyle S_{t}}$ (para qualquer valor de t) é uma variável aleatória com distribuição log-normal com valor esperado e variância dada porː^[2]

${\displaystyle \mathbb {E} (S_{t})=S_{0}e^{\mu t}}$,

${\displaystyle \operatorname {Var} (S_{t})=S_{0}^{2}e^{2\mu t}\left(e^{\sigma ^{2}t}-1\right)}$,

isto é a função de densidade de probabilidade de uma S_t é:

${\displaystyle f_{S_{t}}(s;\mu ,\sigma ,t)={\frac {1}{\sqrt {2\pi }}}\,{\frac {1}{s\sigma {\sqrt {t}}}}\,\exp \left(-{\frac {\left(\ln s-\ln S_{0}-\left(\mu -{\frac {1}{2}}\sigma ^{2}\right)t\right)^{2}}{2\sigma ^{2}t}}\right)}$.

Quando se derivam outras propriedades do MBG, pode-se fazer uso da EDE de que o MBG é a solução, ou a solução explícita dada acima pode ser utilizada. Por exemplo, considere o processo estocástico de log(S_t). Este é um interessante processo, porque no modelo de Black–Scholes ela está relacionada com o log-retorno do preço das ações. Usando o cálculo de Itō com f(S) = log(S) dáː

${\displaystyle {\begin{alignedat}{2}d\log(S)&=f^{\prime }(S)\,dS+{\frac {1}{2}}f^{\prime \prime }(S)S^{2}\sigma ^{2}\,dt\\&={\frac {1}{S}}\left(\sigma S\,dW_{t}+\mu S\,dt\right)-{\frac {1}{2}}\sigma ^{2}\,dt\\&=\sigma \,dW_{t}+(\mu -\sigma ^{2}/2)\,dt.\end{alignedat}}}$

Segue-se que ${\displaystyle \mathbb {E} \log(S_{t})=\log(S_{0})+(\mu -\sigma ^{2}/2)t}$.

Este resultado também pode ser obtido aplicando-se o logaritmo para a solução explícita do MBG:

${\displaystyle {\begin{alignedat}{2}\log(S_{t})&=\log \left(S_{0}\exp \left(\left(\mu -{\frac {\sigma ^{2}}{2}}\right)t+\sigma W_{t}\right)\right)\\&=\log(S_{0})+\left(\mu -{\frac {\sigma ^{2}}{2}}\right)t+\sigma W_{t}.\end{alignedat}}}$

Tomando a expectativa produz o mesmo resultado acima: ${\displaystyle \mathbb {E} \log(S_{t})=\log(S_{0})+(\mu -\sigma ^{2}/2)t}$.

Versão multivariada 

O MBG pode ser estendido para o caso em que há múltiplos caminhos de preços correlacionados.

Cada trajetória de preço segue o processo subjacente

${\displaystyle dS_{t}^{i}=\mu _{i}S_{t}^{i}\,dt+\sigma _{i}S_{t}^{i}\,dW_{t}^{i}}$,

Onde os processos de Wiener estão correlacionados de modo que ${\displaystyle \mathbb {E} (dW_{t}^{i}dW_{t}^{j})=\rho _{i,j}dt}$ onde ${\displaystyle \rho _{i,i}=1}$.

Para o caso multivariado, isso implica que

${\displaystyle \mathrm {Cov} (S_{t}^{i},S_{t}^{j})=S_{0}^{i}S_{0}^{j}e^{(\mu _{i}+\mu _{j})t}\left(e^{\rho _{i,j}\sigma _{i}\sigma _{j}t}-1\right)}$.

Uso em finanças

Ver artigo principal: Black-Scholes

O movimento geométrico browniano é usado para modelar os preços das ações no modelo Black-Scholes e é o modelo mais utilizado no comportamento do preço das ações.^[3]

Alguns dos argumentos para usar o MBG para modelar os preços das ações são:

• Os retornos esperados do MBG são independentes do valor do processo (preço das ações), o que está de acordo com o que seria esperado na realidade.^[3]
• O MBG só assume valores positivos, assim como os preços das ações reais.
• O MBG mostra o mesmo tipo de "rugosidade" em seus caminhos como vemos nos preços das ações reais.
• Cálculos com MBG são relativamente fáceis.

No entanto, MBG não é um modelo completamente realista, em particular, fica aquém da realidade nos seguintes pontos:

• Nos preços das ações reais, a volatilidade muda ao longo do tempo (possivelmente estocasticamente), mas no MBG, a volatilidade é assumida constante.
• Na vida real, os preços das ações geralmente mostram saltos causados ​​por eventos ou notícias imprevisíveis, mas no MBG, o caminho é contínuo (sem descontinuidade).